Newton–Raphson metodoa (Newton-en metodo gisa ere ezagutzen dena) zenbakizko analisi-metodo bat da. Metodo honek funtzioen erro gero eta hobeak lortzen ditu, hau da, funtzioa zero egiten duen x balioa bilatzen du. Beste modu batez esanik, funtzioak OX ardatza mozten duen balioa (funtzioaren erroa) ematen du Newton–Raphson metodoak. Algoritmoa erroaren hurbilketa batekin hasten da eta urrats bakoitzean erroaren hurbilketa hobea lortzen du.
Matematikan funtzio koadratikoa funtzio polinomiko mota bat da, itxura kanonikoan honela definitua:
ax2 + bx + c = 0
Non a, b eta c zenbaki errealak diren (eta a ≠ 0).
Funtzio koadratikoren deribatua lerro zuzena da eta bere integrala funtzio kubikoa da.
Aldagai bakarreko funtzio errealen kasuan honakoa da metodoa:
Izan bedi ƒ funtzioa x errealentzat definitua, eta izan bedi ƒ' bere deribatua. Erroaren hasierako hurbilketa bat behar dugu, x0. Erroaren hurbilketa horretan oinarrituz hurbilketa hobea izango den x1 honelaxe lortzen da:
Iterazioak eginez, n+1 hurbilketa n hurbilketan oinarritzen da formula honen arabera:
Formula horren zergatia geometrikoki adieraz daiteke. Hurrengo irudiko lerro urdina f(x) funtzioa da, eta lerro zuzen gorria f(x) funtzioaren tangentea (xn, f(xn)) puntuan:
Berde koloreko distantziari hobekuntza deitzen badiogu, orduan alfa angeluaren tangentea f(xn)/hobekuntza litzateke, baina tangente hori f(x) funtzioaren deribatua (xn, f(xn))puntuan da, lerro zuzen gorriaren malda alfa angeluaren tangentea da. Horregatik:
tag(alfa)= f(xn)/hobekuntza eta aldi berean tag(alfa)=malda= f'(xn)
beraz f'(xn)= f(xn)/hobekuntza (non hobekuntza=xn-xn+1)
f'(xn)= f(xn)/(xn-xn+1) nondik xn-xn+1= f(xn)/f'(xn)
xn+1 = xn - f(xn)/f'(xn)
ax2+bx+c parabolaren erro bat kalkula dezagun Newton–Raphson metodoa aplikatuz non a, b eta c koefizienteak ezagunak diren. Hona hemen, Newton–Raphson metodotik eratorren formula:
xn+1 = xn - f(xn)/f'(xn)
a, b eta c ezagunak izanik x lortu:
f(x)=ax2+bx+c
f'(x)=2ax+b
xi+1 = xi - f(xi)/f'(xi)
xi+1 = xi - (axi2+bxi+c)/(2axi+b)
Kontu berezia eduki beharko dugu 2axi+b adierazpenaren balioarekin. Ez dugu onartuko zero izatea bestela programa era desegokian bukatuko delako, hots, goiko irudiko tangentea den lerro gorria ezin daiteke horizontala izan (tangente horrek ez luke OX ardatza moztuko).
Erro errealak (bi desberdinak)
Demagun a=1, b=-4 eta c=3 koefizienteak dituen parabolaren erroa kalkulatu nahi dugula. Irudian ikus daitekeen bezala x2-4x+3 parabolaren erroak 1 eta 3 dira. Bestalde, irudian ikusten da ere hurbilketa bezala ez dugula x=2 emango, puntu horretan maldak 0 balio duelako eta lerro horizontalak ez duelako OX ardatza mozten eta ondorioz programak abortatzen duelako.
Hau da ariketaren NewtonErroErrealak.exe programa exekutagarria. Hurbilketa desberdinen araberako programaren hiru irteera hauek erakusten dira jarraian:
Hasierako hurbilketa 2.0000000001 edo handiagoa bada, emaitza 3.0 izango da
Hasierako hurbilketa 1.9999999999 edo txikiagoa bada, emaitza 1.0 izango da
Hasierako hurbilketa 2.0 bada algoritmoak huts egingo du
Zer gertatzen da hurbilketa 1.0 eta 3.0 artean badago (2.0 izan gabe, noski). Adibidez, zer gertatzen da hurbilketa 1.5 bada edo 2.5 bada. Kasu bietan emaitzak zuzenak dira, baina lortuko den erroa lehen hurbilketaren araberakoa da izango da:
- Lehen hurbilketa 1.5 bada, emaitza den erroa 1.0 izango da
- Lehen hurbilketa 2.5 bada, emaitza den erroa 3.0 izango da
Beraz, ikertzen ari garen x2-4x+3 parabolaren kasuan:
- Lehen hurbilketa 2.0 baino txikiagoa bada, emaitza den erroa 1.0 izango da
- Lehen hurbilketa 2.0 baino handiagoa bada, emaitza den erroa 3.0 izango da
- Lehen hurbilketa 2.0 bada, ezin daiteke Newton–Raphson metodoa aplikatu
Erro errealak (bakarra baina doblea)
Demagun a=1, b=0 eta c=-9 koefizienteak dituen parabolaren erroa kalkulatu nahi dugula. Irudian ikus daitekeen bezala x2-9 parabolaren bi erroak 3 dira. Bestalde, irudian ikusten da ere hurbilketa bezala x=3 emango bagenu, puntu horretan malda 0 izan arren programa ondo ibiliko litzatekeela puntu hori soluzioa delako.
Hau da ariketaren NewtonErroErrealak.exe programa exekutagarria. Hurbilketa desberdinen araberako programaren hiru irteera hauek erakusten dira jarraian:
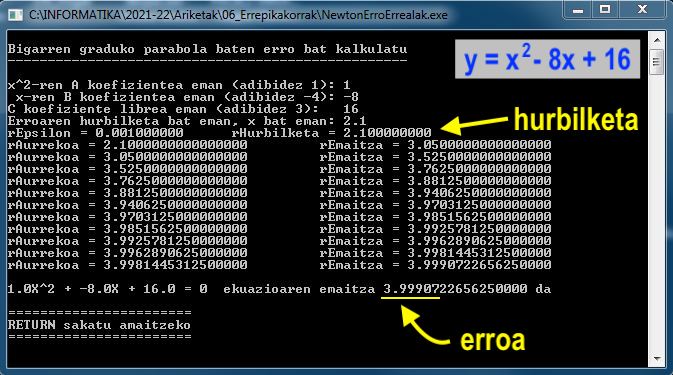
2.1 hasierako hurbilketa 4.0 baino txikiagoa bada, emaitza 4.0 izango da
5.9 hasierako hurbilketa 4.0 baino handiagoa bada, emaitza 4.0 izango da
Hasierako hurbilketa 4.0 bada, iterazioa bakarrarekin 4.0 emaitza lortzen da
Diskriminatzailea negatiboa denean: erro irudikariak
Lerroa horizontala ezin daitekeela izan arestian aipatu dugu, ikus dezagun orain zer gertatzen den ax2+bx+c parabolak OX ardatza ez duenan mozten ezta ikutzen ere ez.
Gogoratu 3. astea | bigarren graduko ekuazioa ariketa non Δ diskriminatzailearen arabera bigarren mailako ekuazio batek soluzio desberdinak izan ditzakeela:
- Δ > 0, diskriminatzailea positiboa bada, bi soluzioak zenbaki erreal dira. Egoera hau aintzakotzat hartzen du aurreko NewtonErroErrealak.exe programak eta arazorik ez da sortzen (baldin eta lerro gorri horizontalik gertatzen ezbada)
- Δ = 0, diskriminatzailea 0 bada, soluzioa bakarra da eta gainera zenbaki erreala. Egoera hau aintzakotzat hartzen du aurreko NewtonErroErrealak.exe programak eta arazorik ez da sortzen (nahiz eta hurbilketa puntuari dagokion lerro gorria lerro horizontala izan, hurbilketa puntu hori soluzioa baita)
- Δ < 0, diskriminatzailea negatiboa bada, ez dago erro errealik eta bi soluzioak zenbaki konplexuak dira eta bata bestearen zenbaki konplexu konjugatu dira. Egoera hau ez du aintzakotzat hartzen aurreko NewtonErroErrealak.exe programak eta programaren exekuzioa ez da eteten, hurrengo adibidearen NewtonEdozeinParabola.exe programa ikusi
Demagun a=1, b=-4 eta c=6 koefizienteak dituen polinomioaren erroa kalkulatu nahi dugula. Irudian ikus daitekeen bezala x2-4x+6 parabolak ez du OX ardatza mozten eta ondorioz erro errealik ez daukala.
x2-4x+6=0 polinomioaren kasuan ez dugu Newton-en metodoa aplikatuko, eta horren ordez bigarren graduko ekuazioaren formula erabiliko dugu:
Hau da ariketaren NewtonEdozeinParabola.exe programa exekutagarria. Programa exekutatzean erro irudikarien kasua erakusten da hemen:
Irudikariak direnean, hurbilketarik ez eskatu eta Newton-en metodoa ez aplikatu
(erro irudikariak bigarren graduko ekuazioaren formularen bitartez lortzen dira)
Balizko soluzio bat programa hau izan daiteke...
NewtonEdozeinParabola.pas
...non rEpsilon doitasuna 0.000000001 konstantea den.















iruzkinik ez:
Argitaratu iruzkina