Arkimedes (Sirakusa, Sizilia, K.a. 287 - toki berean K.a. 212) matematikari, fisikari eta ingeniari greziarra zen. Antzinaroko zientzialari eta matematikari garrantzitsuenetarikotzat jotzen da.
Ziurrenik Arkimedesen ekarpen zientifiko ezagunena bere izena daraman hidrostatikako printzipioa den arren, Arkimedesen Printzipioa, beste arlo batzuetan lan egin zuen, adibidez zirkulu baten zirkunferentziaren eta bere diametroaren arteko erlazioa, gaur egun π (pi) hizkiarekin izendatzen dena.
Zirkunferentzia bati poligono erregularren inskripzio eta zirkunskripzio saioak egin ondoren, π konstantearen balioa finkatu zuen:
Arkimedesek zituen baliabide eskasak kontutan hartuta, lorpen handia izan zen 0,0040% baino errore txikiagoko kalkulua.
Arkimedesen metodoa hexagono erregularra erabiliz
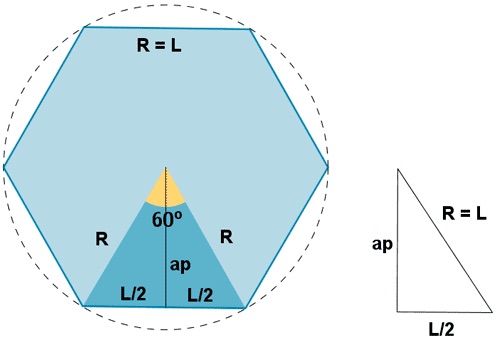
R erradioa duen zirkunferentzia dugula, bi hexagono hartuko ditugu: bat bere barneko hexagono inskribatua eta bestea zirkunferentzia mugatzen duen hexagono zirkunskribatua. Hexagono biren perimetroen artean egongo da 2πR zirkuluaren zirkunferentzia.
Inskribatutako hexagonoa:
Inskribatutako hexagonoaren p perimetroa 6·R da triangelua ekilateroa delako (R=L) eta ondoko hau ikus daiteke, non ap apotema kalkulatzen den:
R = L
p = 6·R (perimetroa)
R2 = R2/4 + ap2
ap2 = R2 - R2/4 = 3·R2/4
ap = √3·R/2 (apotema)
Zirkunskribatutako hexagonoa:
Zirkunskribatutako hexagonoaren P perimetroa kalkulatu behar da, horregatik hexagonoaren A aldea lortu behar da. Irudian ikusten den bezala OXY triangelua eta OX'Y' triangelua antzekoak dira:
R = OX = OY'
X'Y' / XY = OY' / OY (bi triangeluak antzekoak dira)
(A/2) / (R/2) = R / (R·√3/2)
A/R = 2/√3
A = R·2/√3
P = 6·A (perimetroa)
P = R·12/√3 (perimetroa)
Beraz, inskribatutako hexagonoaren p perimetroa R·6 da, eta zirkunskribatutako hexagonoaren P perimetroa R·12/√3 da. Bestalde, R erradioko zirkunferentziari Pz deituz, badakigu bere balioa 2πR dela, non π inkognita den. Bi hexagonoen perimetroak berreskuratuz, argi dago p < Pz < P betetzen dela.
p < Pz < P
R·6 < 2πR < R·12/√3 (zati 2R egitean)
3.0 < π < 6/√3
3.0 < π < 3.4641
Hexagonoa ez ezik, beste poligono batzuekin kalkuluak eginez, esate baterako 12, 24, 48 eta 96 alde dituzten poligonoekin lan eginez, Arkimedesek ondoko balio hau aurkitu zuen π zenbakiarentzat:
Lehenago esan den bezala, emaitzak duen errorea 0,0040% baino txikiagoa da eta kontutan hartuta Arkimedesek zituen baliabideak, lorpen handia izan zela zalantzarik ez dago.





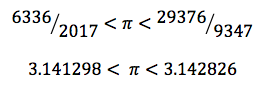
iruzkinik ez:
Argitaratu iruzkina